プログラミングのしかた
前回の後半で基本となる考え方のお話をしました。
・単純化する
・論理的思考
のお話をしました。この2つについて慣れは必要かと思いますがやりだすと慣れてきます。
通常のプログラミングの教科書は、変数はどうだとか、処理の流れがどうだとかをそれぞれのプログラミング言語(プログラムするための文法でできた言語)で教えてくれてます。
でも考え方がわからないのにいきなりこのような話をするといきなり躓きます。そこで、ここからはプログラミングするにあたって現在主流となっている
「構造化プログラミング」と「オブジェクト指向プログラミング」について
何回かにわたってお話します。
あれ?プログラミングを教えてくれるんじゃないの?って思った方。プログラミングの基本的なところで、ここをつかんでおいて、1つの言語を覚えれば、他の言語もすぐにマスターできますので、しばらくお付き合いください。
構造化ってなんか難しそう
『構造化』ってなんか、建設関係の難しい話に聞こえますが、話のベースは簡単なことです。
構造化プログラミングといわれる前のプログラムは、無法地帯のプログラムでした。言い方が悪いことは承知の上で言うと「やりたいようにプログラムする」といようなもので、「とにかく動けばいいんだ、私のやりたいやり方でプログラムする」って感じです。結局、不具合が出るわ、他の人が見たら何してるか理解できないような難解なプログラムでした。
構造化プログラミングは、先に言っている考え方の「単純化する」につながります。何をしてはいけないのかを明確にしていて、プログラムを単純化してます。
基本は3つ
私が昔プログラムを書き始めたころには、goto文というのがありました。(実際まだ一部のプログラム言語では残ってます)これは無条件ジャンプといわれるもので、一気に好きなところに飛んでいける夢のような命令です。これが構造化プログラミングでは「してはいけないこと」になりました。夢が砕けた瞬間です(笑)。
一般社会でも同じですが、何かルールを作らないと人々が好き勝手にやってしまって秩序が乱れます。プログラムの世界ではgotoが秩序を乱していたため、それを使わないようにルール化されたのが構造化プログラミングです。
ただ、それだけではどうしたらよいのかわからなくなるので、3つのルール(構造)が提案されました。
・逐次
・選択
・反復
という3つでプログラムを構成しましょうということです。
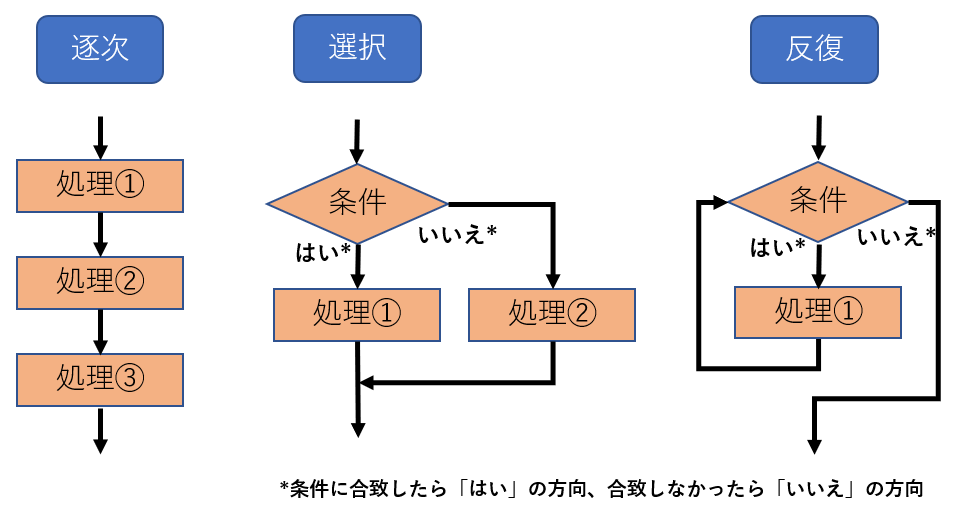
それぞれ図のような流れのものです。
「逐次」
逐次は、単純です。順番に処理しましょうといことで、処理したいものを順番にプログラムしていくだけです。
「選択」
選択は、分かれ道です。人間は目の前に分かれ道があった場合、右に行くか左に行くかを感と経験で決めたりします。でも、何回も言っているようにコンピュータはバカなので感も使えず、経験もありません。
そこで、こういう時は右、こうゆうときは左と教えてあげないといけません。
「反復」
反復は繰り返しです。コンピュータは単純で繰り返しの処理は得意と前に述べました。何千回、何万回の単純な繰り返しも飽きずに疲れも見せずやってくれます。だから、処理を繰り返すようなことをどんどんやらせてみましょう。
なにかこの3つだけで処理が表せるのか不安になりますが、ちゃんとそこは大丈夫です。
私が信じられないと思われても、実際今世の中で動作しているシステム(プログラム)はこれの組み合わせで構成されているからです。難しいことをしているようでも、内部的に細かいところを見てみるとちゃんとこの「逐次」「選択」「反復」が組み合わせっています。
流れはわかりやすく
ものごとを単純化する時に、この3つを意識して単純化していきましょう。前回の例の「1から5まで足した答え」ですが、一番単純には「1に2を足す」「その答えに3を足す」「その答えに4を足す」「その答えに5を足す」と処理をさせると答えが出ます。
これを先の構造化プログラミングで考えると「?を足す」という処理を『逐次』やると答えが出ます。
ただこれだと、100まで足した答えとかもすべてプログラムしなおさないといけません。そこでもう少し考えて、処理を一般化します。
・1から100まで数える
・数えながらその数値を加えていく
というように単純化します。『反復』を使うわけです。そうすると、その100を1万に変えようが、1億に変えようが変更は簡単です。前の『逐次』でやろうとするとプログラムを書く人間の方が死にそうになります(笑)
手順としては
(1)まずは、足していく値を入れておく器を用意する
(2)1から順番に数える、101になったら終わり
(3)数えた数字を器の中の数字に足す
(4)(2)に戻る
だけです。(1)(2)(3)(4)と順番に処理をしていきますが、最後は(2)で終わります。
ポイントは(1)で初めてプログラムするときには思いつかないかもしれません。でもこのようなパターンではまず入れておく器を用意するもなんだと覚えてもらえてらOKです。(後々この器のことを『変数』と呼びますのでちょっと頭の隅においといてください)
また(2)では101になったら終わりと、いきなり100ではなく101が出てきてます。
ここもポイントです。100まで数えるといいながら101で終わりといってます。
100まで足したいので、それより大きくなったら終わりと読み替えないといけません。このあたりも慣れが必要かもしれません。
単純化するにあたってはこのような読み替えが必要になることがあります。ただ、実はそこは本質ではなく、初めで101が100でもいいのです。出てくる答えは間違ってますが、基本となる考えがまずはできているので
そこで今はOKとしましょう。そこを101だとすぐに考えらえるようになってきますので、気にしないでください。
それでもう一度(2)をよく見てください、「101になったら終わり」とあります。全体としては(2)から(4)を『反復』してるのですが、実は(2)は『選択』になってます。(2)は分かれ道になっていて、(3)に数字を足す処理に行く場合と、「終わり」になる場合があります。それを判断するのが、順番に数えていった数字で、それが101になった時だけ「終わり」を選択します。
またまた、よく見ると(1)から(2)や(3)から(4)は『逐次』になっていて必ず順番に処理が行われます。なのでこの処理も3つの構造が組み合わさっているのがわかるかと思います。
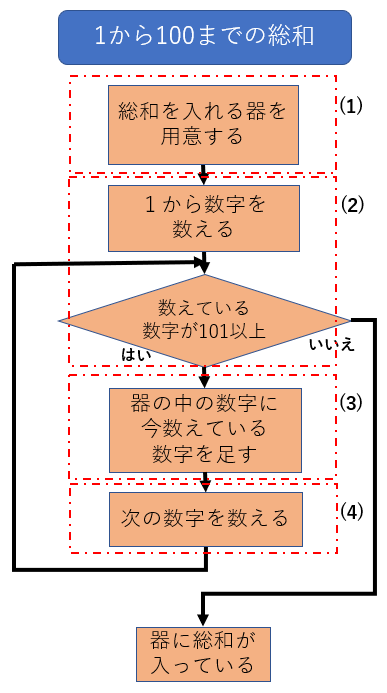
これを図にしてみました。処理的にはもう少し細かく分けてますが、(1)~(4)と示しているところが上の手順です。
図を見てもらえば、逐次、選択、反復が含まれているのがわかるかと思います。
今回のポイント
今回のポイントは、物事を単純化するにあたって『逐次』『選択』『反復』の組み合わせに分解して
考えるということです。それがそのままプログラムの処理にすることができます。
だんだん簡単そうな気になってきてませんか?
それでは次回「オブジェクト指向」について説明したいと思います。
何かこれも難しい言葉を使ってますが、世界一簡単なオブジェクト指向の解説を目指して
書いてみますのでご期待ください。









コメント